Earth's average SW absorbed solar energy: Jsw.not-reflected.average = 111 W/m²
A planet reflects incoming short wave solar radiation. A planet's surface has reflecting properties.
1. The planet's albedo "a". It is a surface quality dependent value.
2. The planet's spherical shape. For a smooth planet the solar irradiation reflection is (0,53 + Φ*a)Jincoming.
What we had till now:
Jsw.incoming - Jsw.reflected = Jsw.not-reflected
Here
Jsw.absorbed = (1-a)*Jsw.incoming
And
Jsw.reflected = a*Jsw.incoming
What we have now is the following:
Jsw.incoming - Jsw.reflected = Jsw.not-reflected
Φ = (1-0,53) = 0,47
Φ = 0,47
Φ is the planet's spherical surface solar irradiation accepting factor.
Jsw.reflected = (0,53 + Φ*a) * Jsw.incoming
And
Jsw.not-reflected = Φ* (1-a) * Jsw.incoming
Where
(0,53 + Φ*a) + Φ* (1-a) = 0,53 + Φ*a + Φ - Φ*a =
= 0,53 + Φ = 0,53 + 0,47 = 1
Conclusion:
A planet's not-reflected fraction of the SW incoming radiation in total is:
Jsw.not-reflected = 0,47*(1-a)*Jsw.incoming
For Planet Earth
Average albedo a = 0,306
Solar flux So = 1.361 W/m²
Jsw.not-reflected = Φ*(1-a)*So =
Jsw.not-reflected = 0,47*(1-0,306)*1.361 W/m² =
= 0,47*0,694*1.361 W/m² = 444,26 W/m²
Averaged on the entire Earth's surface we obtain:
Jsw.not-reflected.average = [ 0,47*(1-a)*1.361 W/m² ] /4 =
= [ 0,47*0,694*1.361 W/m² ] /4 = 444,26 W/m² /4 =
= 111,07 W/m²
Jsw.not-reflected.average = 111 W/m²
The false "RADIATIVE equilibrium" CONCEPT - November 16, 2022
The false "RADIATIVE equilibrium" CONCEPT - November 16, 2022
Also, I should note that the average solar flux is a pure mathematical abstraction.
Solar flux does not average over the planet surface in the real world.
When we "imagine" solar flux averaging on the entire planet surface it is like having (the false RADIATIVE equilibrium CONCEPT), it is like having the actual planet being enclosed in an imaginary sphere, which sphere is emitting towards the planet surface a constant flux of 240 W/m^2.
But it is not what happens in the real world!
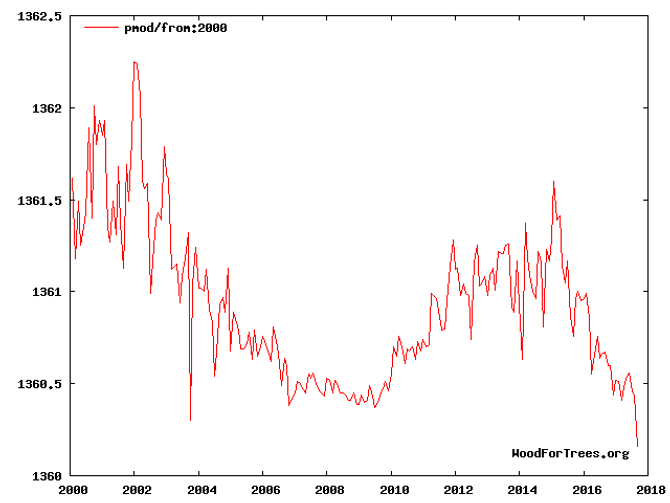
Solar irradiation on the Top Of Atmosphere, http://www.woodfortrees.org/graph/pmod/from:2000
About the satellites’ measurements – they are excellent, I never doubt, I believe in satellites’ measurements
About the satellites’ measurements – they are excellent, I never doubt, I believe in satellites’ measurements.
What I would like to say is that satellites are not capable to “see”, satellites are not capable to measure the reflected from a planet’s surface solar short waves radiation.
The reflected from a planet’s surface solar short waves radiation never reach the satellites high resolution sensors, and therefore the reflected from a planet’s surface solar short waves radiation cannot be measured.
What satellites can “see” and measure is the planet’s albedo.
Albedo is not a primer solar SW radiation reflection.
Albedo is a surface quality, it is a secondary reflection and it is seen and measured by the satellites’ sensors.
Sun's reflection is blinding. Sun's reflection is not seen from the space.
![Figure 13 shows the monthly running annual mean incoming solar radiation following [5] (purple curve) and the global mean TOR (green curve) for the period 2000–2018. The TOR is obtained as the sum of the OLR and the RSR. https://www.mdpi.com/2072-4292/11/6/663/htm](/____impro/1/onewebmedia/i285978589389394105.jpg?etag=%221b68c-5db44839af051%22&sourceContentType= "Figure 13 shows the monthly running annual mean incoming solar radiation following [5] (purple curve) and the global mean TOR (green curve) for the period 2000–2018. The TOR is obtained as the sum of the OLR and the RSR. https://www.mdpi.com/2072-4292/11/6/663/htm")
Figure 13 shows the monthly running annual mean incoming solar radiation following [5] (purple curve) and the global mean TOR (green curve) for the period 2000–2018. The TOR is obtained as the sum of the OLR and the RSR. https://www.mdpi.com/2072-4292/11/6/663/htm
https://www.cristos-vournas.com
The faster a planet rotates (n2>n1) the higher is the planet’s average (mean) temperature T↑mean:
Tmin↑→ T↑mean ← T↓max
.