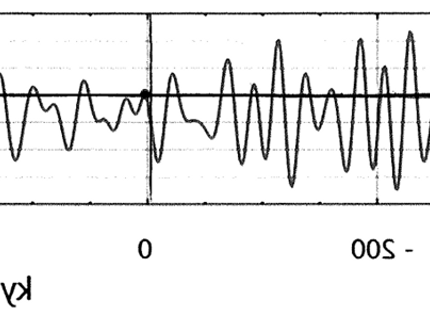
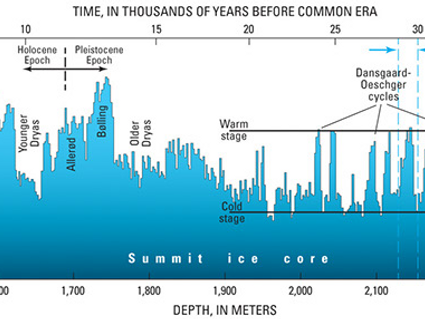
Ice age CO2 reductions coincide with an increase in ice sheet extent
“Ice age CO2 reductions coincide with an increase in ice sheet extent and therefore an increase in global albedo, and this should result in further cooling of the climate. But what actually happens is that when CO2 reaches a minimum and albedo reaches a maximum, the world rapidly warms into an interglacial. A similar effect can be seen at the peak of an interglacial, where high CO2 and low albedo results in cooling. This counterintuitive response of the climate system also remains unexplained, and so a hitherto unaccounted for agent must exist that is strong enough to counter and reverse the classical feedback mechanisms.”
https://www.sciencedirect.com/science/article/pii/S1674987116300305?via%3Dihub
The REVERSED Milankovitch Cycle (Backwards)
SUMMIT ICE CORE
Jemit.planet = 4πr²σΤmean⁴ /(β*N*cp)¹∕ ⁴ (W)
The ~288K is not Earth’s uniform equilibrium temperature.
The ~288K is Earth’s average surface temperature.
Earth’s surface doesn’t emit IR radiation out to space at that temperature (~288K).
The every infinitesimal spot and at the every infinitesimal space of time emits at different intensity (W/m^2).
And, consequently, every infinitesimal spot and at every infinitesimal space of time emits at different temperature Tχ (K).
When integrated over the entire planet’s sphere area and over the 24 hours long day-night solar irradiation cycle the total planet’s emission energy will be
Jemit.planet = Jemit1 + Jemit2 + …+ Jemitχ
χ → ∞
or, maybe better like this
Jemit.planet = { [ dA1*σΤ1⁴ /(β*N*cp)¹∕ ⁴ + dA2*σΤ2⁴ /(β*N*cp)¹∕ ⁴ + …+ dAχ*σΤχ⁴ /(β*N*cp)¹∕ ⁴ ]dt1 + [ dA*1σΤ1⁴ /(β*N*cp)¹∕ ⁴ + dA2*σΤ2⁴ /(β*N*cp)¹∕ ⁴ + …+ dAχ*σΤχ⁴ /(β*N*cp)¹∕ ⁴ ]dtψ +… + etc } / χΣ dtψ
dAχ → 0, Σ dAχ = 4πr² (m²)
dtψ → 0, Σ dtψ = 24 hours
χ → ∞
And, after integration
Jemit.planet = 4πr²σΤmean⁴ /(β*N*cp)¹∕ ⁴ (W)
Consequently
Earth’s surface doesn’t emit
Jemit = 4πr²σ288K⁴ (W)
But Earth’s surface emits
Jemit = 4πr²σ288⁴ /(β*N*cp)¹∕ ⁴ (W)
We are not justified to average
Jemit = 4πr²σ288⁴ /(β*N*cp)¹∕ ⁴ (W) over the entire surface and to write
Jemit = σ288⁴ (W/m^2)
because surface doesn’t emit on average temperature. Thus, the result is very much different.
Jemit.earth = 4πr²σ288⁴ /(β*N*cp)¹∕ ⁴ (W)
Planet Energy Budget:
Jabs = Jemit
πr²Φ*S*(1-a) = 4πr²σTmean⁴ /(β*N*cp)¹∕ ⁴ (W)
Solving for Tmean we obtain the Planet Mean Surface Temperature Equation:
Tmean.planet = [ Φ (1-a) S (β*N*cp)¹∕ ⁴ /4σ ]¹∕ ⁴ (K)
Let’s calculate Tmean.earth
So = 1.361 W/m² (So is the Solar constant) S (W/m²)
is the planet’s solar flux.
For Earth S = So
Earth’s albedo: aearth = 0,306
Earth is a smooth rocky planet, Earth’s surface solar irradiation accepting factor Φearth = 0,47 (Accepted by a Smooth Hemisphere with radius r sunlight is S*Φ*π*r²(1-a),
where Φ = 0,47)
β = 150 days*gr*oC/rotation*cal – is a Rotating Planet Surface Solar Irradiation INTERACTING-Emitting Universal Law constant
N = 1 rotation /per day, is Earth’s axial spin
cp.earth = 1 cal/gr*oC, it is because Earth has a vast ocean.
Generally speaking almost the whole Earth’s surface is wet.
We can call Earth a Planet Ocean.
σ = 5,67*10⁻⁸ W/m²K⁴, the Stefan-Boltzmann constant Earth’s Without-Atmosphere Mean Surface Temperature Equation Tmean.earth is:
Tmean.earth= [ Φ (1-a) So (β*N*cp)¹∕ ⁴ /4σ ]¹∕ ⁴
Τmean.earth = [ 0,47(1-0,306)1.361 W/m²(150 days*gr*oC/rotation*cal *1rotations/day*1 cal/gr*oC)¹∕ ⁴ /4*5,67*10⁻⁸ W/m²K⁴ ]¹∕ ⁴ =
Τmean.earth = [ 0,47(1-0,306)1.361 W/m²(150*1*1)¹∕ ⁴ /4*5,67*10⁻⁸ W/m²K⁴ ]¹∕ ⁴ =
Τmean.earth = ( 6.854.905.906,50 )¹∕ ⁴ = 287,74 K
Tmean.earth = 287,74 Κ
When we apply the Tmean.planet equation
Tmean.planet = [ Φ (1-a) S (β*N*cp)¹∕ ⁴ /4σ ]¹∕ ⁴ (K)
by substituting the terms (Φ, S, N, cp) for each different planet, then we calculate the planets’ mean surface temperatures, and they match very closely with the planets’ mean surface temperatures measured by satellites.
Planet………..Te…………Tmean….Tsat.mean
Mercury….439,6 K…….325,83 K…..340 K
Earth………255 K………287,74 K…..288 K
Moon……..270,4 Κ……..223,35 Κ…..220 Κ
Mars……209,91 K……..213,21 K…..210 K
The black body temperature of a planet concept
THE BLACK BODY TEMPERATURE THEORY (An old over simplifying and misleading concept)
"The temperature that the surface of a body (such as a planet, like the Earth) would be if it were not warmed by its own atmosphere. It can be calculated using the Stefan–Boltzmann equation. The black body temperature of the Earth is -18°C, but the actual surface temperature is about 15°C."
THE MISTAKEN CONCLUSION
"The difference (33°C) is the amount by which the planet is warmed by the absorption of radiation within its atmosphere, by the natural greenhouse effect."
.
.
.
.
.